Menguasai Dunia Tiga Dimensi: Contoh Soal Matematika Bangun Ruang Kelas SD Semester 2

Semester kedua di bangku Sekolah Dasar (SD) seringkali membawa petualangan baru dalam dunia matematika, salah satunya adalah eksplorasi bangun ruang. Jika sebelumnya kita lebih banyak bermain dengan bidang datar, kini saatnya menyelami objek-objek yang memiliki volume dan ruang. Memahami konsep bangun ruang sangat penting karena ini adalah dasar untuk banyak konsep matematika yang lebih kompleks di jenjang selanjutnya, serta membantu anak-anak mengembangkan pemahaman spasial dan kemampuan memecahkan masalah.

Artikel ini akan menjadi panduan lengkap bagi orang tua dan guru dalam membantu siswa kelas SD menguasai materi bangun ruang di semester 2. Kita akan membahas berbagai jenis bangun ruang yang umum diajarkan, beserta contoh-contoh soal yang bervariasi, mulai dari yang paling dasar hingga yang sedikit menantang.

Mengapa Bangun Ruang Penting?

Sebelum kita masuk ke contoh soal, mari kita pahami mengapa topik ini begitu krusial:

• Pemahaman Spasial: Anak-anak belajar mengenali, membedakan, dan membayangkan bentuk-bentuk tiga dimensi di sekitar mereka. Ini membantu mereka dalam membaca peta, memahami diagram, bahkan dalam aktivitas sehari-hari seperti menyusun mainan.
• Konsep Volume dan Luas Permukaan: Bangun ruang memperkenalkan konsep volume (ruang yang ditempati objek) dan luas permukaan (jumlah luas semua sisi luar objek). Ini adalah dasar untuk perhitungan yang lebih lanjut.
• Keterampilan Pemecahan Masalah: Soal-soal bangun ruang seringkali membutuhkan analisis, penalaran, dan penerapan rumus, yang semuanya melatih kemampuan pemecahan masalah.
• Koneksi dengan Dunia Nyata: Bangun ruang ada di mana-mana: kotak, bola, kaleng, rumah, gedung pencakar-gedung. Memahaminya membuat anak lebih peka terhadap lingkungan sekitar.

Bangun Ruang Umum di Kelas SD Semester 2

Pada umumnya, siswa kelas SD semester 2 akan diperkenalkan pada beberapa bangun ruang dasar, yaitu:

1. Kubus: Bangun ruang yang memiliki enam sisi persegi yang sama besar. Semua rusuknya sama panjang.
2. Balok: Bangun ruang yang memiliki enam sisi persegi panjang. Sisi-sisi yang berhadapan memiliki ukuran yang sama.
3. Prisma Segitiga: Bangun ruang yang memiliki alas dan tutup berbentuk segitiga yang kongruen (sama dan sebangun), serta sisi-sisi tegak berbentuk persegi panjang.
4. Tabung (Silinder): Bangun ruang yang memiliki alas dan tutup berbentuk lingkaran yang kongruen, serta sisi tegak berbentuk persegi panjang jika dibuka.
5. Kerucut: Bangun ruang yang memiliki alas berbentuk lingkaran dan titik puncak.
6. Bola: Bangun ruang yang semua titik permukaannya berjarak sama dari titik pusatnya.

Rumus-Rumus Dasar yang Perlu Diketahui

Sebelum mengerjakan soal, penting untuk mengingat beberapa rumus dasar. Untuk kelas SD, fokus biasanya pada volume.

• Kubus:
  • Volume (V) = sisi × sisi × sisi = s³
• Balok:
  • Volume (V) = panjang × lebar × tinggi = p × l × t
• Prisma Segitiga:
  • Volume (V) = Luas alas × tinggi prisma
  • Luas alas segitiga = ½ × alas segitiga × tinggi segitiga
  • Jadi, V = (½ × alas segitiga × tinggi segitiga) × tinggi prisma
• Tabung:
  • Volume (V) = Luas alas × tinggi
  • Luas alas lingkaran = π × jari-jari² (πr²)
  • Jadi, V = π × r² × t
  • Catatan: Nilai π biasanya diberikan sebagai 22/7 atau 3,14.
• Kerucut:
  • Volume (V) = ⅓ × Luas alas × tinggi
  • Luas alas lingkaran = π × r²
  • Jadi, V = ⅓ × π × r² × t
• Bola:
  • Volume (V) = ⁴⁄₃ × π × r³

Contoh Soal dan Pembahasannya

Mari kita mulai dengan contoh-contoh soal yang mencakup berbagai bangun ruang.

1. Soal Kubus

Soal 1: Sebuah kubus memiliki panjang rusuk 8 cm. Berapakah volume kubus tersebut?

Pembahasan:
Untuk mencari volume kubus, kita menggunakan rumus V = s³.
Diketahui panjang rusuk (s) = 8 cm.
V = 8 cm × 8 cm × 8 cm
V = 64 cm² × 8 cm
V = 512 cm³

Jawaban: Volume kubus tersebut adalah 512 cm³.

Soal 2: Volume sebuah kubus adalah 1.000 cm³. Berapakah panjang rusuk kubus tersebut?

Pembahasan:
Kita tahu V = s³.
1.000 cm³ = s³
Untuk mencari s, kita perlu mencari akar pangkat tiga dari 1.000.
s = ³√1.000 cm³
s = 10 cm

Jawaban: Panjang rusuk kubus tersebut adalah 10 cm.

2. Soal Balok

Soal 1: Sebuah kotak mainan berbentuk balok memiliki panjang 15 cm, lebar 10 cm, dan tinggi 12 cm. Berapakah volume kotak mainan tersebut?

Pembahasan:
Rumus volume balok adalah V = p × l × t.
Diketahui p = 15 cm, l = 10 cm, t = 12 cm.
V = 15 cm × 10 cm × 12 cm
V = 150 cm² × 12 cm
V = 1.800 cm³

Jawaban: Volume kotak mainan tersebut adalah 1.800 cm³.

Soal 2: Sebuah akuarium berbentuk balok memiliki volume 12.000 cm³. Jika panjangnya 40 cm dan lebarnya 20 cm, berapakah tinggi akuarium tersebut?

Pembahasan:
Rumus volume balok adalah V = p × l × t.
Kita memiliki V = 12.000 cm³, p = 40 cm, l = 20 cm. Kita perlu mencari t.
12.000 cm³ = 40 cm × 20 cm × t
12.000 cm³ = 800 cm² × t
Untuk mencari t, kita bagi volume dengan hasil perkalian panjang dan lebar:
t = 12.000 cm³ / 800 cm²
t = 15 cm

Jawaban: Tinggi akuarium tersebut adalah 15 cm.

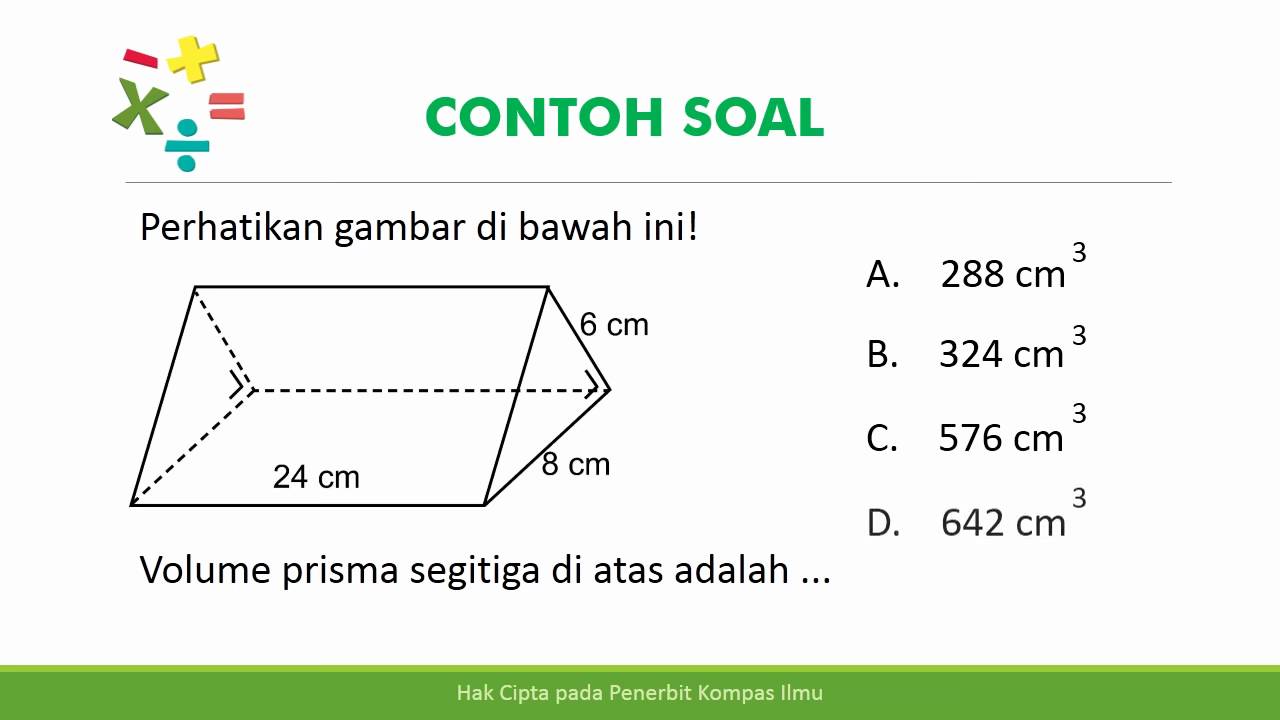
3. Soal Prisma Segitiga

Soal 1: Sebuah tenda berbentuk prisma segitiga memiliki alas segitiga dengan panjang alas 10 cm dan tinggi segitiga 6 cm. Tinggi prisma tenda tersebut adalah 15 cm. Berapakah volume tenda tersebut?

Pembahasan:
Rumus volume prisma segitiga adalah V = Luas alas × tinggi prisma.
Luas alas segitiga = ½ × alas segitiga × tinggi segitiga
Luas alas = ½ × 10 cm × 6 cm
Luas alas = ½ × 60 cm²
Luas alas = 30 cm²

Sekarang kita hitung volume prisma:
V = Luas alas × tinggi prisma
V = 30 cm² × 15 cm
V = 450 cm³

Jawaban: Volume tenda tersebut adalah 450 cm³.

4. Soal Tabung

Soal 1: Sebuah kaleng minuman berbentuk tabung memiliki jari-jari alas 7 cm dan tinggi 10 cm. Jika π = 22/7, berapakah volume kaleng tersebut?

Pembahasan:
Rumus volume tabung adalah V = π × r² × t.
Diketahui r = 7 cm, t = 10 cm, π = 22/7.
V = (22/7) × (7 cm)² × 10 cm
V = (22/7) × 49 cm² × 10 cm
Kita bisa menyederhanakan 49 dibagi 7 menjadi 7.
V = 22 × 7 cm² × 10 cm
V = 154 cm² × 10 cm
V = 1.540 cm³

Jawaban: Volume kaleng minuman tersebut adalah 1.540 cm³.

Soal 2: Sebuah drum minyak berbentuk tabung memiliki diameter 28 cm dan tinggi 30 cm. Jika π = 22/7, berapakah volume drum tersebut?

Pembahasan:
Pertama, kita perlu mencari jari-jari (r) dari diameter. Jari-jari adalah setengah dari diameter.
Diameter = 28 cm, jadi r = 28 cm / 2 = 14 cm.
Rumus volume tabung adalah V = π × r² × t.
Diketahui r = 14 cm, t = 30 cm, π = 22/7.
V = (22/7) × (14 cm)² × 30 cm
V = (22/7) × 196 cm² × 30 cm
Kita bisa menyederhanakan 196 dibagi 7. 196 ÷ 7 = 28.
V = 22 × 28 cm² × 30 cm
V = 616 cm² × 30 cm
V = 18.480 cm³

Jawaban: Volume drum minyak tersebut adalah 18.480 cm³.

5. Soal Kerucut

Soal 1: Sebuah topi ulang tahun berbentuk kerucut memiliki jari-jari alas 7 cm dan tinggi 12 cm. Jika π = 22/7, berapakah volume topi tersebut?

Pembahasan:
Rumus volume kerucut adalah V = ⅓ × π × r² × t.
Diketahui r = 7 cm, t = 12 cm, π = 22/7.
V = ⅓ × (22/7) × (7 cm)² × 12 cm
V = ⅓ × (22/7) × 49 cm² × 12 cm
Sederhanakan 49 dibagi 7 menjadi 7.
V = ⅓ × 22 × 7 cm² × 12 cm
V = ⅓ × 154 cm² × 12 cm
Sekarang, sederhanakan 12 dibagi 3 menjadi 4.
V = 22 × 7 cm² × 4 cm
V = 154 cm² × 4 cm
V = 616 cm³

Jawaban: Volume topi ulang tahun tersebut adalah 616 cm³.

6. Soal Bola

Soal 1: Sebuah bola memiliki jari-jari 6 cm. Jika π = 3,14, berapakah volume bola tersebut?

Pembahasan:
Rumus volume bola adalah V = ⁴⁄₃ × π × r³.
Diketahui r = 6 cm, π = 3,14.
V = ⁴⁄₃ × 3,14 × (6 cm)³
V = ⁴⁄₃ × 3,14 × (6 cm × 6 cm × 6 cm)
V = ⁴⁄₃ × 3,14 × 216 cm³
Kita bisa menyederhanakan 216 dibagi 3. 216 ÷ 3 = 72.
V = 4 × 3,14 × 72 cm³
V = 12,56 × 72 cm³
V = 904,32 cm³

Jawaban: Volume bola tersebut adalah 904,32 cm³.

Tips Tambahan untuk Membantu Siswa

• Visualisasi: Gunakan benda nyata berbentuk bangun ruang (kotak, bola, tabung) untuk membantu siswa memvisualisasikan konsep.
• Gambar: Dorong siswa untuk menggambar bangun ruang dan melabeli bagian-bagiannya (rusuk, sisi, alas, tinggi, jari-jari).
• Latihan Berulang: Semakin banyak latihan, semakin terbiasa siswa dengan rumus dan cara penyelesaiannya.
• Soal Cerita: Buat soal cerita yang relevan dengan kehidupan sehari-hari siswa agar mereka melihat aplikasi nyata dari matematika.
• Fokus pada Konsep: Pastikan siswa memahami arti dari volume, bukan hanya menghafal rumus.

Memahami bangun ruang adalah perjalanan yang menyenangkan dan mendidik bagi siswa SD. Dengan latihan yang terarah dan pemahaman konsep yang kuat, mereka akan mampu menaklukkan soal-soal matematika tiga dimensi ini dengan percaya diri. Selamat belajar!

>